1.10 Farbmetrik
Bei der Farbmetrik ist das wesentliche Problem die Quantifizierung der physiologischen Farbwahrnehmung bedingt durch die sogenannte spektrale Farbreizfunktion φλ(λ). Zur Bestimmung der Farbe einer primären Lichtquelle, kommt φλ(λ) dem spektralen Strahlungsfluss Φλ(λ) der Quelle gleich (oder einer anderen spektralen radiometrischen Größe wie Strahlstärke oder Strahldichte). Um die Farbe eines reflektierenden oder transmittierenden Objektes (z. B. eines Filters) zu bestimmten, wird φλ(λ) mit der einfallenden spektralen Bestrahlungsstärke, die auf die Objektoberfläche auftritt, gleichgesetzt. Daraufhin wird diese mit dem spektralen Reflexionsgrad, dem Strahldichtekoeffizienten oder dem spektralen Transmissionsgrad des Objektes multipliziert. Da Farben reflektierender oder transmittierender Objekte von der Beleuchtungsstärke der Objekte abhängen, hat die CIE farbmetrische Normlichtarten festgelegt. Die Normlichtart A der CIE ist durch einen Planck’schen Schwarzkörperstrahler bei einer Farbtemperatur von 2856 K definiert. Die Normlichtart D56 der CIE entspricht dem mittleren Tageslicht bei einer korrelierten Farbtemperatur von 6500 K (eine Definition von Farbtemperatur wird im weiteren Verlauf gegeben).
Die folgenden Abschnitte bieten Informationen zu:
RGB- und XYZ-Spektralwertfunktionen
Gemäß der Tristimulus-Theorie kann jede Farbe, die vom durchschnittlich normal sehenden Auge wahrgenommen wird, mit drei Zahlen beschrieben werden. Diese geben die Reizgröße von roten, grünen und blauen Zäpfchen an. Resultieren zwei Farbreize in den gleichen Werten für diese drei Reizgrößen, erzeugen sie – auch bei unterschiedlicher spektraler Verteilung – die gleiche Farbwahrnehmung. Wright und Guild haben um 1930 herum Untersuchungen durchgeführt, bei denen Beobachter Licht von 435,8 nm, 546,1 nm und 700 nm derart kombinieren sollten, dass die dadurch hervorgerufene Farbwahrnehmung derjenigen entspricht, die durch monochromatisches Licht bei einer gewissen Wellenlänge des sichtbaren Spektrums erzeugt wird. Die Auswertung dieser Untersuchungen wurden in der Definition der standardisierten RGB-Spektralwertfunktionen r(λ), g(λ) und b(λ) festgehalten. Diese wurden von der CIE im Jahr 1931 in die XYZ-Spektralwertfunktionen x(λ), y(λ) und z(λ) umgewandelt. Diese Spektralfunktionen definieren den farbmetrischen Normalbeobachter CIE 1931 und gelten für eine Gesichtsfeldgröße von 2°. In der Praxis kann der Normalbeobachter für jedes Gesichtsfeld, das kleiner als 4° ist, eingesetzt werden. Bei einem Gesichtsfeld von 10° kommen andere von der CIE spezifizierte Spektralwertfunktionen zum Einsatz: x10(λ), y10(λ) und z10(λ). Diese Funktionen legen den ergänzenden farbmetrischen Normalbeobachter CIE 1964 fest, der bei Gesichtsfeldern von mehr als 4° eingesetzt wird.

Abb. 1: XYZ-Spektralwertfunktionen gemäß des farbmetrischen Normalbeobachters CIE 1931.
x(λ) (schwarze Volllinie) besteht aus einem kurzen und einem langen Wellenlängenabschnitt und
y(λ) (graue Volllinie) ist identisch mit der spektralen Empfindlichkeitsfunktion V(λ) der CIE.
Die RGB- und XYZ-Spektralwertfunktionen können gleichermaßen zur Bestimmung der drei Parameter, deren jeweilige Zahlen eine gewisse Farbwahrnehmung beschreiben, herangezogen werden. Dabei werden jedoch die XYZ-Spektralwertfunktionen bevorzugt, da sie positive Werte für alle Wellenlängen aufweisen (s. Abb. 1). Zusätzlich ist y (λ) identisch zur spektralen Empfindlichkeitsfunktion V(λ) der CIE für photopisches Sehen.
Die XYZ-Tristimulus-Werte einer bestimmten Spektralwertfunktion φλ(λ) werden mittels
X = k ∫ φλ(λ) · x (λ) dλ λ
Y = k ∫ φλ(λ) · y (λ) dλ λ
Z = k ∫ φλ(λ) · z (λ) dλ λ
berechnet.
Die Wahl der Normalisierungskonstante k ist mit der farbmetrischen Aufgabenstellung verknüpft: Beschreibt die Spektralwertfunktion φλ(λ) eine spektrale radiometrische Größe einer primären Lichtquelle, dann entspricht k = 683 lm/W und Y liefert somit die entsprechende photometrische Größe. Gibt die Spektralwertfunktion φλ(λ) die spektrale Verteilung von optischer Strahlung, die von einem Objekt reflektiert oder durchgegeben wird, an, so ist k definiert durch
k = 100 ∫ Eλ(λ) y (λ) dλ λ
Dabei beschreibt E(λ) die einfallende Bestrahlungsstärke, die auf die Objektoberfläche auftrifft.
x-y- und u'-v'-Farbortkoordinaten
Obwohl die XYZ-Tristimulus-Werte einen dreidimensionalen Farbraum mit allen möglichen Farbwahrnehmungen abbilden, ist für viele Anwendungsfälle eine zweidimensionale Ebene der Farbdarstellung oftmals ausreichend. Eine zweidimensionale Darstellung ist etwa durch die x-y-Farbortkoordinate der CIE von 1931 mit den Koordinaten x und y gegeben, die anhand der Projektion der X-, Y- und Z-Werte berechnet werden:
x = X X + Y + Z
y = Y X + Y + Z
Die x-y-Farbortkoordinate wird zwar weitestgehend benutzt, birgt aber den großen Nachteil, dass in dieser geometrische Differenzstrecken nicht mit den wahrgenommenen Farbunterschieden übereinstimmen. Aus diesem Grund hat die CIE 1976 die Farbortkoordinate u', v' gemäß UCS-Farbraum festgelegt, wobei ihre Koordinaten folgendermaßen bestimmt werden:
u' = 4X X + 15Y + 3Z
v' = 9Y X + 15Y + 3Z
Obwohl die definierten Koordinaten u' und v' keine strikte Übereinstimmung zwischen geometrischen Differenzstrecken und wahrgenommenen Farbunterschieden liefern, weisen sie doch deutlich weniger Unstimmigkeiten als die x-y-Farbortkoordinate der CIE auf.

Abb. 2: x, y CIE 1931 Farbortkoordinate
Basierend auf (Stand 2002): http://home.wanadoo.nl/paulschils/10.02.htm

Abb. 3: u', v' CIE 1976 Farbortkoordinate
Basierend auf (Stand 2002): http://home.wanadoo.nl/paulschils/10.02.htm
Korrelierte Farbtemperatur
Mit der korrelierten Farbtemperatur wird die spektrale Verteilung von optischer Strahlung emittiert von einer Lichtquelle beschrieben. Diese Beschreibung entspricht der Projektion einer zweidimensionalen Farbortkoordinate auf eine eindimensionale Ebene und ist daher nur ein ungefähres Maß.
D. h., die korrelierte Farbtemperatur wird in Kelvin (K) angegeben und ist die Temperatur des Planck’schen Schwarzkörperstrahlers. Die dort empfangene Farbe ähnelt sehr stark einem gegebenen Farbreiz.
Als vereinfachte Faustregel kann festgehalten werden, dass spektrale Verteilung, die von langen (rötlichen) Wellenlängen gelenkt wird, einer niedrigen korrelierten Farbtemperatur entspricht und spektrale Verteilung, die von kurzen (bläulichen) Wellenlängen gelenkt wird, eine hohe korrelierte Farbtemperatur aufweist. Beispielsweise besitzt die warmweiße Farbe einer Glühlampe eine korrelierte Farbtemperatur von circa 2800 K, normales Tageslicht weist eine korrelierte Farbtemperatur von etwa 6500 K auf und die bläulich-weiße Farbe einer Kathodenstrahlröhre (CRT) etwa 9000 K.
Farbwiedergabeindex CRI
Der Farbwiedergabeindex (color rendering index, CRI) ist die numerische Beschreibung der Farbwiedergabe-Qualität einer Lichtquelle bei gleicher korrelierter Farbtemperatur. Hierbei beschreibt der allgemeine Farbwiedergabeindex Ra einen Mittelwert der ersten acht Testtafeln. Insgesamt existieren derzeit 14 Testtafeln, welche von der DIN 6169 sowie CIE 13.2 festgelegt wurden. Oftmals wird auch noch ein CRI 15 berechnet, der nachträglich hinzugefügt wurde. Für die Berechnung wird die Farbtemperatur bis 5000 K eines Schwarzkörperstrahlers verwendet, über 5000 K wird die tageslichtähnliche Verteilung der D65 (D65 = 6500 K Daylight) herangezogen. Grundsätzlich lässt sich sagen, dass der Farbwiedergabeindex nicht von der Farbtemperatur abhängt, sondern nur von der spektralen Verteilung relativ zur Referenzlichtquelle innerhalb des sichtbaren Spektralbereichs. Mathematisch ergibt sich der Ra aus:
Ra = 1/8 Σ8i=1 Ri'
wobei Ri aus
Ri = 100 - 4,6 · Δ Ei
berechnet wird. Hierbei ist ΔEi der euklidische Abstand zwischen der entsprechenden Testtafel beleuchtet mit dem Teststrahler sowie der Referenz. In der folgenden Grafik sind die spektralen Verläufe der Testtafeln dargestellt.
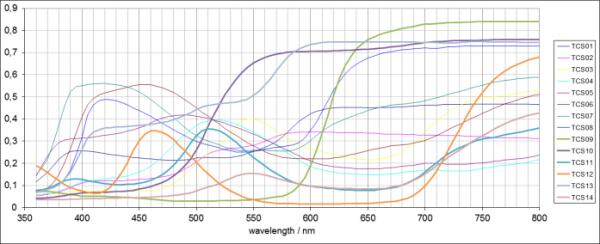
Abb. 4: Testtafeln nach CIE 13.2
Farbpräferenz-Farbwiedergabemetrik CQS
Neben den CRI der CIE 1976 gibt es auch die 15 CQS (Color Quality Scale) Testtafeln, welche vergleichbar berechnet werden. Die CQS-Methode (Version 7.5) verwendet 15 speziell ausgewählte (gesättigte) Testfarben aus dem Munsell- Farbsystem statt der CIE-Testfarben. Der CIEFarbwiedergabeindex bewertet solche Testlichtquellen mit einem niedrigeren Wert, die die Sättigung der Objektfarbe im Vergleich zur Referenzlichtquelle erhöhen. Um eine Tendenz der Farbpräferenz der Beobachter (nämlich die Präferenz der gesättigten Farben) zu berücksichtigen, bewertet die CQS-Methode die Erhöhung der Sättigung durch den Teststrahler im Vergleich zur Referenz in der CQS-Methode nicht negativ. Eine erhöhte Sättigung unter dem Teststrahler im Vergleich zur Referenz bedeutet, dass sich die Farbwahrnehmung des Objektes ändert, d. h., keine Übereinstimmung zwischen dem Teststrahler und Referenz besteht, was von einem Farbwiedergabeindex immer negativ bewertet werden muss. Darum stellt die CQS-Metrik per Definition keine Farbwiedergabemetrik dar, sondern eine kombinierte Farbpräferenz-Farbwiedergabemetrik. Die CQS ist eine kombinierte Farbpräferenz- Farbwiedergabemetrik und keine reine Farbwiedergabemetrik. D. h., sie bietet den Vorteil, das Farbpräferenzen berücksichtigt werden. Der Nachteil allerdings besteht darin, dass die objektive Bewertung verfälscht wird.
Planck’scher Kurvenzug
Der Planck’sche Kurvenzug (Planckian Locus) zeigt den Kurvenverlauf eines Schwarzkörperstrahlers im Farbdiagramm gemäß den Farbtemperaturen an.
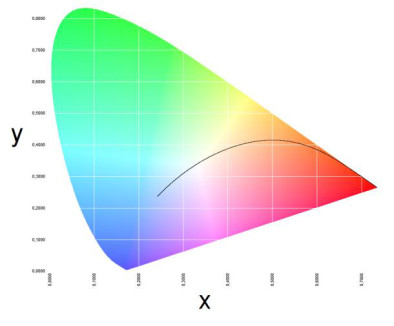
Abb. 5: Planck’scher Kurvenzug
Die dominante Wellenlänge eines Strahlers
Die dominante Wellenlänge eines Strahlers ergibt sich aus dem Schnittpunkt der Geraden definiert durch den Weißpunkt (Unbuntpunkt) und den Messpunkt. D. h., die dominante Wellenlänge entspricht der Wellenlänge auf dem Spektralkurvenzug des CIE-Diagramms, an dem die Gerade den Kurvenzug schneidet. Dies ist folgend im CIE-Farbraum dargestellt (s. Abb. 6). Die dominante Wellenlänge kann nicht direkt aus dem Spektrum abgelesen werden. Es ist eine Aussage, welche mit der Farbmetrik bewertet ist.
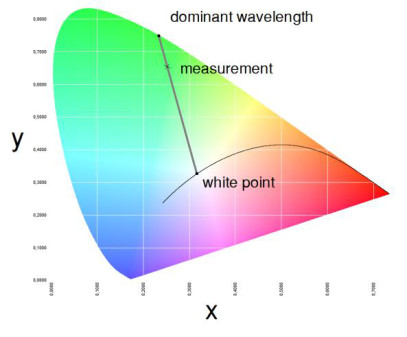
Abb. 6: Dominante Wellenlänge in der CIE 1931-Farbtafel
Die Farbreinheit eines Strahlers (purity)
Die Farbreinheit (engl. purity) gibt an, wie nahe ein Strahler dem spektralen Kurvenzug der CIE-Farbtafel liegt. Geometrisch lässt sie sich wie folgt darstellen:

Abb. 7: Purity in der CIE 1931-Farbtafel
Das Kreuz stellt den Farbort der Messung dar. Die Linie wird gezeichnet von Weißpunkt (Unbuntpunkt) durch den Farbort zur dominanten Wellenlänge der Messung. Hierbei berechnet sich die Farbreinheit nun aus den Teilstrecken zu:
Farbreinheit = a a + b'
wobei a die Strecke von Weißpunkt (Unbuntpunkt) zu Messpunkt und b die Strecke von Messpunkt zu dominanter Wellenlänge ist. Ist die Farbreinheit gleich eins und somit die Strecke b gleich Null, so handelt es sich um eine reine spektrale Linie, z. B. eine Laserlinie. Ist die Farbreinheit gleich Null, so handelt es sich um einen Strahler mit einem maximal breiten Spektrum.
MacAdams Ellipsen und Binning-Felder
Die Farbabstände im x-y-Farbraum, der 1931 entstand, entsprechen nicht den wahrgenommenen Abständen des Menschen. D. h., liegen zwei Messpunkte im Farbraum gleich weit von einem beliebigen Bezugspunkt entfernt, so wird der Farbkontrast unterschiedlich stark wahrgenommen. Diese Erkenntnis versuchte MacAdam (1942) durch seine Ellipsen zu berücksichtigen. Diese werden meist als n-fache MacAdam-Ellipsen genutzt, wobei n der Vergrößerung relativ zu den ursprünglichen Ellipsen entspricht. Gängig für n ist z. B. 5x und 10x.

Abb. 8: MacAdam-Ellipsen in der XY-Farbtafel
Die Untersuchungen von MacAdam waren ein großer Fortschritt und mit den damaligen Möglichkeiten (Versuchsaufbauten und Computerleistung) durchaus bemerkenswert. In den 1960er-Jahren wurden weitere Untersuchungen vorangetrieben, woraus dann später auch der CIE 1976 u‘-v‘-Farbraum entstand. Die CIE empfiehlt den u'-v'-Farbraum zu nutzen, auch wenn der x-y-Farbraum der noch am weitesten verbreitete ist.

Abb. 9: MacAdam-Ellipsen in der u'v'-Farbtafel
Neue Erkenntnisse zeigen, dass die Ellipsen für neue Technologien (SSL (Solid State Lightning)) in der Halbleiterlichtbranche wie LED nicht mehr ideale sind. Denn die Ellipsen wurden mittels Fluoreszenzlampen sechs verschiedener Farbtemperaturen bestimmt. Mit den neuen Technologien ist diese Einschränkung nicht mehr gegeben, d. h., für diese Vielfältigkeit werden neue Vorschriften benötigt, wie z. B. die ANSI (ANSI NEMA ANSLG. 2011. C78.377-2008) mit acht nominellen CCTs sowie flexiblen CCTs in 100 K Abständen:

Abb. 10: ANSI Felder in der u'-u'-Farbtafel
Die neuste Empfehlung der CIE besteht darin, n-fache u'v'-Kreise zu nutzen, welche auf den Mittelpunkten der MacAdam-Ellipsen (IEC 60081, IEC 1997) liegen und deren Radius angepasst werden kann. Diese Kreise können mathematisch beschrieben werden:
( u' - u'c )2 + ( v' - v'c )2 = (0,0011 · n)2
Mit dieser Beschreibung ist es nun auch möglich, Interpolationen in der CCT durchzuführen, welche die Vielfältigkeit der LED Technologien widerspiegeln.
Für das Binning werden diese Felder oder vom Hersteller eigens definierte Felder genutzt, um ihre LEDs nach gewissen Farbeigenschaften zu selektieren und sortieren. Für diese Art der Messungen sind sehr genaue Spektrometer, d. h., in erster Linie Wellenlängengenauigkeit, geringe optische Bandbreite (oder Geräte mit Bandbreitenkorrektur) sowie qualifizierter Absolutkalibrierung nötig. Hinzu kommen eine hohe Empfindlichkeit und eine Elektroniktechnologie des Gerätes, welche schnelle Messungen und Datenübertragungen ermöglicht. Erfüllt ein Messgerät diese Anforderungen, so erlaubt es präzise und schnelle Messungen, welche im LED-Binning benötigt werden.
In der folgenden Graphik sind Binning-Felder eines LED Herstellers dargestellt.
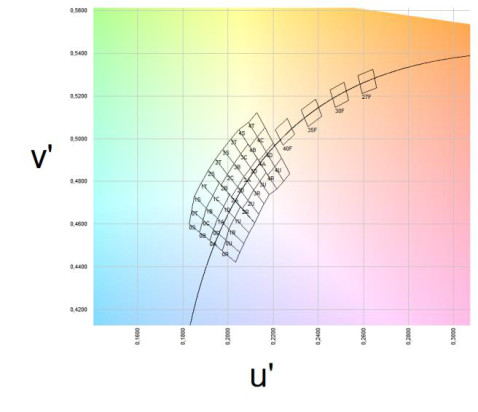

Abb. 11: verschiedene Binning-Felder